Vetores
Vetor é em sua definição mais simples uma seta desenhada em escala usada para representar uma grandeza vetorial (possui módulo e orientação, tal como força).
Adição de dois vetores
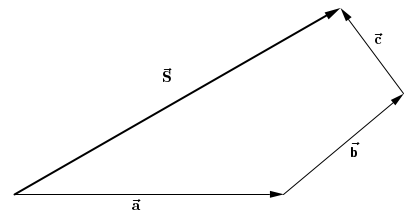
O Método Poligonal pode ser utilizado para a soma de dois ou mais vetores. Podemos representar esta soma traçando um vetor partindo da origem do primeiro vetor e terminando na extremidade do último vetor. Isto está representado na figura abaixo onde a soma é dita por \(\vec{S}\) onde \(\vec{S} = \vec{a}+\vec{b}+\vec{c}\).
Já Regra do Paralelograma serve para somar apenas dois vetores.
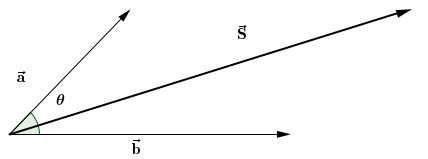
Para calcular o módulo desta soma devemos observar o valor do ângulo \(\theta\):
$$\theta = 0°\rightarrow\vec{S}=\vec{a}+\vec{b}$$ $$\theta = 180° \rightarrow \vec{S}=\vec{a}-\vec{b}$$ $$\theta = 90° \rightarrow |\vec{S}|^{2}=|\vec{a}|^{2}+|\vec{b}|^{2}$$ $$\theta \neq 0°, 90° \,ou\, 180° \rightarrow |\vec{S}|^{2}=|\vec{a}|^{2}+|\vec{b}|^{2} +2.a.b.cos\theta$$ $$\theta = 120° \text{e}\ |\vec{a}|=|\vec{b}| \ \text{então}\ |\vec{S}|^{2}=|\vec{a}|^{2}=|\vec{b}|^{2}$$Sistema Referencial
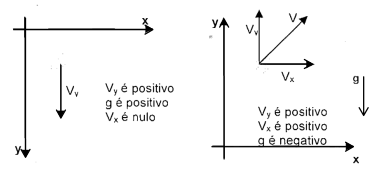
Movimento e repouso: Movimento e repouso são conceitos relativos, pois dependem do referêncial adotado. Um sistema referencial bem definido, com uma, duas ou três dimensões, é importante não apenas para se observar o movimento ou repouso de um corpo, mas principalmente para orientar e organizar as grandezas envolvidas. As grandezas são positivas quando apontam no sentido crescente do eixo referencial e negativas quando apontam no sentido oposto.
$$\text{Progressivo: } v>0$$ $$\text{Retrógrado: } v<0$$ $$\text{Acelerado: } v.a>0 \rightarrow |v| \text{ aumenta}$$ $$\text{Retardado: }v.a<0 \rightarrow |v| \text{ diminui}$$Exemplos de Sistemas Referenciais:
Cinemática Escalar
1.1 Movimento Retilíneo Uniforme (M.R.U)
O que caracteriza o M.R.U é o corpo apresentar:
$$v = \text{constante} \neq 0$$ $$a = 0$$ $$v = v_{m} = \frac{\Delta S}{\Delta t}$$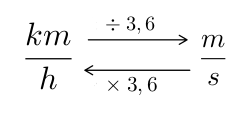
1.2 Equação Horária do M.R.U
$$S = S_{0} + v.\Delta t$$2.1 Movimento Retilíneo Uniformemente Variado (M.R.U.V)
Apresentam M.R.U.V corpos sujeitos a uma aceleração constante e não nula na direção do movimento:
$$a = \text{constante} \neq 0$$ $$a = a_{m} = \frac{\Delta v}{\Delta t}$$2.2 Equações do M.R.U.V
$$v = v_{0} + a.t \rightarrow (v \text{ versus }t)$$ $$S = S_{0} + v_{0}.t + \frac{a.t^{2}}{2} \rightarrow (S \text{ versus }t)$$ $$v^{2} = v^{2}_{0} + 2.a.\Delta S \rightarrow (v \text{ versus } S)$$Para obter os dados a partir dos gráficos use:
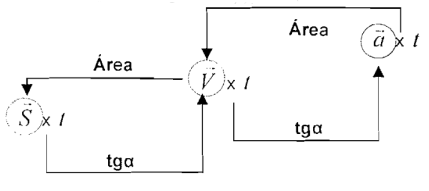
3. Gráfico do M.R.U e M.R.U.V
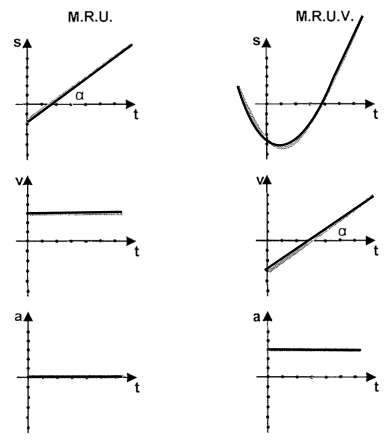
4. Ultrapassagens
No estudo de ultrapassagens o ponto crítico a ser observado é o momento em que os corpos estão emparelhados, isto é, quando \(S_{A}=S_{B}\) onde:
$$S_{A,B} = S_{0_{(A,B)}} +v_{A,B}.t$$ $$S_{A,B} = S_{0_{(A,B)}} + v_{0_{(A,B)}}.t + \frac{a_{(A,B)}.t^{2}}{2}$$5. Velocidade Relativa (inclusive vetorial)
Seja \(\vec{V_{A}}\) a velocidade de um corpo A em relação ao solo e \(\vec{V_{B}}\) a velocidade de um corpo B em relação ao solo, então a velocidade de A em relação a B, \(\vec{V_{AB}}\), pode ser descrita como:
$$\vec{V_{AB}}= \vec{V_{A}} - \vec{V_{B}}$$Movimento em Duas e Três Dimensões
Princípio de Galileu:
Quando um corpo realiza um movimento em várias direções simultaneamente podemos estudar o movimento de cada direção separadamente como se os demais não existissem.

Lançamentos
1. Vertical:
No lançamento vertical deve-se dar atenção ao referencial adotado para não errar sinais nas contas, uma vez que temos duas situações possíveis:
1.1 Lançamento Vertical para cima:
Onde \({v_{y}}_{0}\) e \(g\) apresentam, obrigatóriamente sinais opostos:
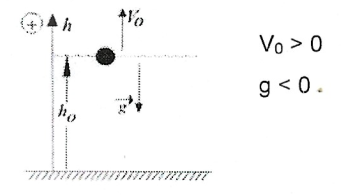
1.2 Lançamento Vertical para baixo
Onde \({v_{y}}_{0}\) e \(g\) apresentam, obrigatóriamente sinais iguais:

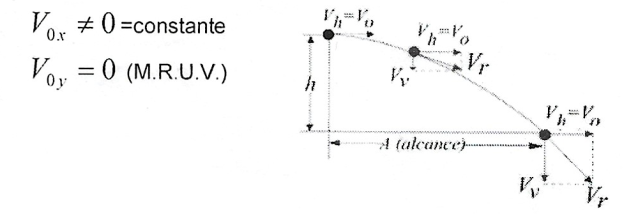
2. Horizontal:
Trata-se de um lançamento em duas dimensões onde a velocidade inicial do corpo apresenta componentes não nulas apenas na direção horizontal e ainda, o movimento na direção vertical será acelerado enquanto o horizontal é uniforme. Desta forma:
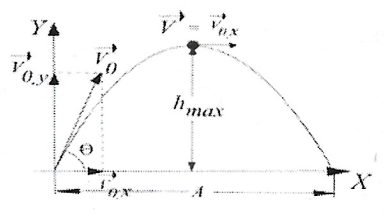
3. Lançamento Obliquo
É uma composição de M.R.U.V na direção vertical e M.R.U na horizontal com \(v_{0} \neq 0\) em ambas as direções. A trajetória, sem resistência do ar, deve ser parabólica.
Movimento Circular
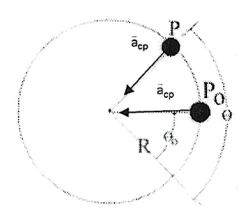
1. Movimento Circular Uniforme
Trata-se de um movimento com velocidade \(v\) constante, mas que apresenta uma aceleração de direção perpendicular a esta velocidade (ambos possuem módulo constante). Assim, em um movimento circular temos:
2. Movimento Circular Uniformemente Variado
Ocorre quando a aceleração vetorial não é perpendicular nem paralela ao vetor tangencial do móvel. Assim, esta pode ser decomposta nas componentes tangencial e radial, de tal forma que a soma destas acelerações se definem:
$$\vec{a} = \vec{a}_{t} + \vec{a}_{cp}$$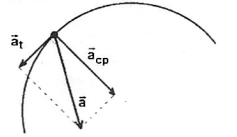
3. Movimento Retilíneo *versus* Movimento Circular
As equações destes movimentos são análogas e estão resumidas na tabela abaixo:
| Movimento Retilíneo | Movimento Circular |
| \(S = S_{0} +v.t\) | \(\theta = \theta_{0} +\omega.t\) |
| \(S = S_{0} + v_{0}.t + \frac{a}{2}.t^{2}\) | \(\theta = \theta_{0} + \omega_{0}.t + \frac{\vec{a_{t}}}{2}.t^{2}\) |
| \(v = v_{0} + a.t\) | \(\omega = \omega_{0} + \vec{a_{t}}.t\) |
| \(v^{2} = {v_{0}}^{2} +2.a.\Delta S\) | \(\omega^{2} = {\omega_{0}}^{2} +2.\vec{a_{t}}.\Delta \theta\) |
4. Movimento Circular: Polias e Engrenagens
Sistemas de polias compartilhando correias ou engrenagens conectadas devem apresentar mesma velocidade tangencial, logo:
$$v_{A} = v_{B}$$ $$2.\pi.R_{A}.f_{A}=2.\pi.R_{B}.f_{B}$$ $$f_{A} = \frac{R_{B}}{R_{A}}.f_{B} \\ \text{ ou } \\ T_{A} = \frac{R_{A}}{R_{B}}.T_{B}$$Duas engrenagens A e B qualquer, com número total \(N_{A}\) e \(N_{B}\) de dentes pode ter seu movimento observado contanto o respectivo \(N\) em uma volta completa de \(2.\pi.R_{n}\), dessa forma têm-se:
$$N_{A}.f_{A}=N_{B}.f_{B}$$Discos compartilhando o mesmo eixo central para rotação devem apresentar mesma velocidade angular, logo:
$$\omega_{A}=\omega_{B}$$ $$\frac{v_{A}}{R_{A}}=\frac{v_{B}}{R_{B}}$$Movimento Harmônico Simples
O Movimento Harmônico Simples, também conhecido como M.H.S, pode ser definido como sistema que oscila sem que ocorra discipações de energia para o ambiente de forma que seu período seja uniforme. As equações do M.H.S são expressas como:
$$s = A.cos(\theta_{0}+\omega.t)$$ $$v = -A.\omega.sen(\theta_{0}+\omega.t)$$ $$a = -A.\omega^{2}.cos(\theta_{0}+\omega.t)=-A.\omega^{2}$$1. Oscilador Massa-Mola
É dado por um corpo oscilando exclusivamente devido à força de restituição elástica.
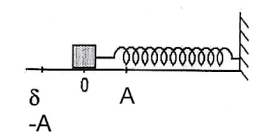
2. Pêndulo Simples
Um corpo oscilando no ar (sem resistência) caracteriza um pêndulo simples. As equações podem ser escritas como:
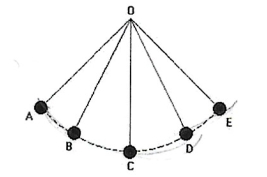
2.1 Pêndulo Cônico
Um Pêndulo Cônico éum sistema onde um corpo dependurado por um fio desenvolve um movimento circular em um plano horizontal fazendo um ângulo \(\theta\) com a vertical tal qual a figura abaixo:
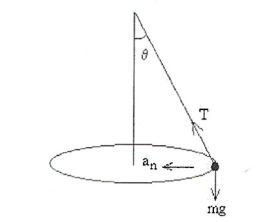
O período deste pêndulo é expresso na forma:
$$T = 2.\pi.\sqrt{\frac{l.cos\theta}{g}}$$Dinâmica
É importante ressaltar que uma Lei na ciência é uma hipótese ou afirmação geral a respeito da relação entre quantidades naturais, e que tem sido testada inúmeras vezes sem ser negada.
Leis de Newton
1. Primeira Lei - Inércia
Todo objeto mantém-se em repouso ou em movimento teilíneo com velocidade uniforme a menos que sobre ele seja exercida uma Força resultante não nula. - Newton
A Lei da inércia prevê que todo corpo que apresenta resultante de Forças externas nula deve manter sua velocidade constante, seja esta nula, \(v=0\), ou não, \(v=\text{constante = M.R.U}\).
2. Segunda Lei - Princípio Fundamental
A aceleração de um objeto é diretamente proporcional à Força resultante atuando sobre ele; Possui o mesmo sentido que essa Força e é inversamente proporcional à massa do objeto. - Newton
A segunda Lei mostra que a resultante das Forças externas apliaca sobre um corpo pode ser nula, ou quando existe aceleração:
3. Terceira Lei - Ação e Reação
Para toda força aplicada (ação) surgirá uma outra força (reação) de mesma intensidade na mesma direção, mas de sentido oposto. - Newton
4. Tipos de Forças
Força em sua maneira mais simples é um empurrão ou puxão agindo sobre um objeto como resultado de sua interação com outro objeto. Existem vários tipos de Força e podemos colocar em duas grandes categorias, Forças de Contato e Forças de Campo. Porém vale ressaltar que na natureza existe fundamentalmente apenas 4 tipos de forças, sendo elas:
gravitacional, eletromagnética, nuclear forte, nuclear fraca.
4.1 Força de Campo
São forças que podem ser aplicadas mesmo quando não existe contato direto entre os corpos do sistema, como por exemplo Força Graviational - Força Elétrica - Força Magnética - Força Nuclear.
4.2 Forças de Contato
Históricamente chama-se de Forças de Contato quando há a necessidade de existir contato entre os objetos para que a Força exista. Contúdo, não existem forças de contato, uma vez que todas as manifestações surgem mediante a interações das 4 forças fundamentais ditas anteriormente, o que são Forças de Campo.
No contexto de nosso estudo podemos chamar essas Forças de Contato como Forças Mecânicas, algumas delas são:
Normal - Força de reação ao contato entre superfícies, sempre perpendicular ao plano tangente às superfícies. Vale ressaltar que não é a reação ao Peso.
Tração - É a Força existente nos fios e cordas quando estes são esticados - tracionados - tencionados.
Atrito - A Força de Atrito sempre se opõe ao movimento ou à tendência do movimento dos corpos. Devemos atentar que $$F_{at}(estático)>F_{at}(dinâmico)$$ ou seja, o atrito dos corpos em repouso é maior que quando estes estão em movimento. A Força de Atrito pode ser calculado pela expressão: $$F_{at}=\mu.N$$ onde \(\mu\) é o coeficiente de atrito, e \(N\) é a Normal dos corpos em contato.
- Elástica - A Força Elástica é uma força de restituição, isto é, ela sempre é oposta a deformação s causada no corpo em questão. Esta força respeita a Lei de Hooke: $$F=k.s$$ onde k é a constante elástica da mola (ou elśtico) e deve ser medido em N/m no SI. Molas que estejam associadas irão distribuir as forças de tensão entre elas, isto segundo a terceira Lei de Newton. Para encontrar o valor de uma mola equivalente usamos as seguintes equações: $$\text{Em série: }\frac{1}{k_{eq}}=\frac{1}{k_{1}}+\frac{1}{k_{2}}+...+\frac{1}{k_{n}}$$ $$\text{Em paralelo: } k_{eq}=k_{1}+k_{2}+...+k_{n}$$
Polias e Plano Inclinado
1. Polias
As polias quando fixas podem alterar a direção ou o sentido de um movimento ou de uma força. Entretanto, se esta for móvel, então além de desviar a direção e/ou sentido, também faz com que a força se divida da seguinte forma:
$$F= \frac{P}{2^{n}}$$onde \(n\) é o número de polias móvias do sistema.
2. Plano Inclinado
O eixo \(X\) e \(Y\) saem de seu padrão horizontal e vertical, respectivamente, para acompanhar a inclinação do plano (conservando a perpendicularidade entre ambos). Dessa forma, podemos observar o movimento apenas na direção \(X\) devido a decomposição da força Peso em duas componentes.
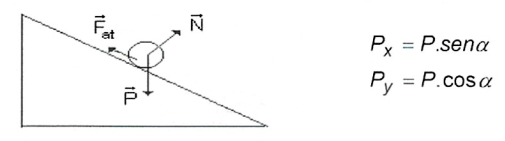
- Importante : Devemos atentar que nesta situação a Força Normal deve ser aplicada na nova direção do eixo \(Y\) tornando no caso mais simples $$|\vec{N}| = |\vec{P_{y}}|$$ Assim, sempre que precisarmos do módulo da Normal (por exemplo para calcular a força de atrito) deveremos tomar o valor correto.
Blocos
Para resolver exercícios envolvendo blocos com sucesso devemos seguir os seguintes passos:
- Desenhe todos os corpos envolvidos separadamente, para melhor visualizar as Forças externas atuantes.
- Faça o diagrama de Forças para cada corpo identificando todas elas.
- Aplique a Segunda Lei de Newton em cada corpo separadamente obtendo uma equação para cada um deles
- Resolva o sistema de equações obtido de forma a encontrar as variáveis desejadas
Dinâmica do Movimento Circular
Sempre em um movimento circular seja ele uniforme ou não, deve existir uma força resultante centrípeta responsável pelo surgimento da aceleração centrípeta, que pode ser expressa por: $$F_{cp}=m.a_{cp} = \frac{m.v^{2}}{R}=m.\omega^{2}.R$$ Devemos nos lembrar do fato desta força ser uma resultante de forças, isto é, não existe uma força efetivamente centrípeta e sim uma resultante de forças radialmente centrípeta. Desta forma, todas as forças estudadas (Forças de Campo e de Contato) serão utilizadas para resolver estes exercícios.
Estática
É a parte da Física que estuda sistemas (partículas ou corpos rígidos) sob a ação de forças em equilíbrio. $$\sum \vec{F}_{ext} = 0$$ $$\sum \vec{M}_{0} = 0$$
Torque
Torque, também conhecido como Momento de uma Força, é o efeito de rotação causado por uma Força: $$\vec{M}_{0} = \vec{F}.\vec{d}.sen\theta$$
Centro de Massa
A posição média da massa de um objeto. O ***Centro de Massa (CM)*** move-se como se todas as forças externas atuassem neste ponto. Suas coordenadas podem ser dadas por: $$X_{CM} = \frac{X_{1}.M_{2} + X_{2}.M_{2}+...+X_{N}.M_{N}}{M_{1}+M_{2}+...+M_{N}}$$ $$Y_{CM} = \frac{Y_{1}.M_{2} + Y_{2}.M_{2}+...+Y_{N}.M_{N}}{M_{1}+M_{2}+...+M_{N}}$$ $$Z_{CM} = \frac{Z_{1}.M_{2} + Z_{2}.M_{2}+...+Z_{N}.M_{N}}{M_{1}+M_{2}+...+M_{N}}$$ Lembrando que em corpos homogêneos o centro de massa é o baricentro e em corpos homogêneos e simétricos é o centro geométrico.
Gravitação
Leis de Kepler
1. Lei das Órbitas
Todos os planetas se movem em órbitas elípticas em torno do Sol, o qual ocupa um dos focos.
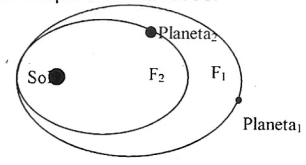
2. Lei das Áreas
O vetor raio que une o Sol a um planeta varre áreas iguais no plano da órbita em tempos iguais.
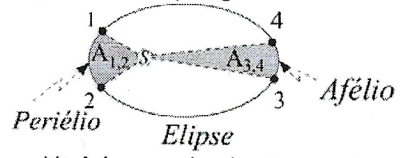
Portanto a área varrida A é proporcional ao tempo \(\Delta t\), ou seja: $$\frac{A_{1,2}}{A_{3,4}}=\frac{\Delta t_{1,2}}{\Delta t_{3,4}}$$
3. Lei dos Períodos
O quadrado dos períodos, \(T\), de revolução (volta) dos planetas em torno do Sol são proporcionais ao cubo dos raios médios, \(R\), de suas órbitas.
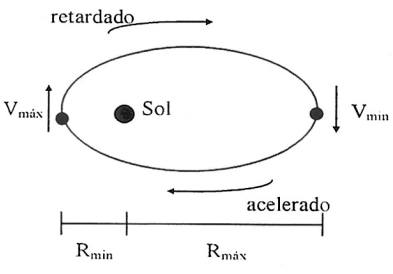
- Observação - A constante k é uma constante característica de cada sistema solar, e apresenta um valor aproximado de 1,0 para o nosso sistema solar.
4. Gravitação Universal de Newton
Qualquer partícula no Universo atrai outra partícula segundo a equação: $$F_{g} = G.\frac{M.m}{R^{2}}$$
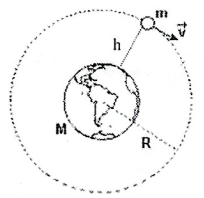
- Campo Gravitacional - O Campo gravitacional \(\vec{g}\) depende inversamente da distância entre os centros de massa dos corpos. É semppre comum relacionar a força de atração universal de Newton com Peso ou com uma Resultante Centrípeta, nestes casos temos:
| Gravitação e Peso | Gravitação e Resultante Centrípeta |
| \(g =\frac{G.M}{R^{2}}\) | \(v=\sqrt{\frac{G.M}{R}}\) |
Impulso e Quantidade de Movimento
1. Quantidade de Movimento
A quantidade de movimento de um corpo está relacionada a sua massa inercial, assim: $$\vec{Q} = m.\vec{v}$$
2. Impulso
Quando aplicamos uma força sobre um corpo ou sistema de corpos durante um intervalo de tempo, provocamos uma variação na quantidade de movimento deste: $$\vec{I} = \Delta \vec{Q}$$ $$\vec{I}=\vec{F}.\Delta t$$
3. Colisões
A quantidade de movimento de um sistema isolado é invariante, logo: $$\Delta \vec{Q} = 0$$ $$\vec{Q}_{antes}=\vec{Q}_{depois}$$ Durante as colisões pode haver conservação de Energia Cinética ou não. Devido esta perda de energia o coeficiente \(e\), coeficiente de restituição elástica, é dado por: $$e=\frac{v'_{B}-v'_{A}}{v_{A}-v_{B}}$$
3.1 Colisão Inelástica
Não ocorre conservação de energia cinética e apresenta \(e=0\).
3.2 Colisão Parcialmente Elástica
Não ocorre conservação de energia cinética e apresenta \(0\lt e\lt1\)
3.3 Colisão Perfeitamente Elástica
Ocorre conservação de energia cinética e apresenta \(e=1\).
3.4 Colisão Super Elástica
Não ocorre conservação de energia cinética e apresenta \(e>1\). Este é um caso especial onde a energia final é maior que a inicial, logo, para que esta ocorra é necessário que exista uma fonte de energia externa.
Trabalho e Energia Mecânica
1. Trabalho
É uma expressão de energia dada, somente se a força for constante, por: $$W = \tau =F.d.cos\theta$$

No caso de \(F\) não ser constante, o trabalho pode ser calculado pela área do gráfico \(F\) versus \(d\):
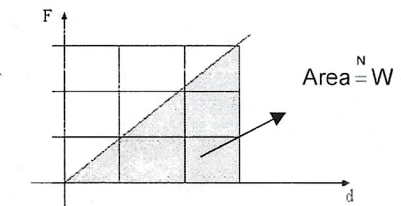
2. Energia Mecânica
É definida como a soma entre as ***energias cinéticas*** (*energia de movimento*) e ***energia potências*** (*energia que um corpo possui por causa de sua posição*) ou ***sistema em questão***: $$E_{Mec} = E_{cin} + E_{pot} = E_{cin} + E_{pot_{gravit}} + E_{pot_{elást}}$$ $$E_{cin} = \frac{m.v^{2}}{2}$$ $$E_{pot_{gravit}} = m.g.h$$ $$E_{pot_{elást}} = \frac{k.s^{2}}{2}$$
- Sistema Conservativo - Em um sistema conservatico a Energia Mecânica total não se dissipa, logo: $$\Delta E_{Mec} = 0$$ $$E_{Mec_{inicial}} = E_{Mec_{final}}$$
- Sistema Não-Conservativo - Em um sistema não conservativo, parte da Energia Mecânica total se dissipa, logo: $$\Delta E_{Mec}= E_{diss}$$ $$E_{Mec_{inicial}} = E_{Mec_{final}} + E_{diss}$$
3. Trabalho e Energia Mecânica
Em um sistema não conservativo a Energia Mecânica dissipada geralmente está relacionada ao trabalho de uma força resistiva. Desta forma: $$\Delta E_{cin} = W = \tau$$ $$\Delta E_{pot_{gravit}} = -W = -\tau$$
4. Potência e Rendimento
Pode ser definida pela quantidade de trabalho (motor ou resistente) que um corpo ou sistema pode realizar em um determinado intervalo de tempo: $$P = \frac{W}{\Delta t}= \frac{E}{\Delta t}$$ Como em um sistema real a energia total \(E_{t}\) de um sistema nunca é convertida integralmente em trabalho havendo sempre uma dissipação \(E_{diss}\), podemos calcular o rendimento observado a parcela de energia útil, \(E_{u}\), efetivamente convertida em trabalho: $$\eta = \frac{E_{u}}{E_{t}} = \frac{P_{u}}{P_{t}}$$ $$E_{t} = E_{u} + E_{diss}$$ $$P_{t} = P_{u} + P_{diss}$$
Hidrostática
Densidade
É a razão entre a massa e o volume de um corpo, sendo expresso como \(\mu = \frac{m}{V}\)
Pressão
Quando aplicamos uma força \(F\) sobre ums superfície de uma área \(A\), exercemos uma pressão sobre essa igual a: $$P = \frac{F}{A}$$
- Pressão de uma coluna de um líquido - Devido ao peso do liquído acumulado sobre uma superfície, este exercerá uma pressão sobre a superfície na forma: $$P = \mu_{liq}.g.h$$ onde \(h\) representa a altura da coluna do liquido. Em caso de a coluna estar exposta à atmosfera aberta, então a pressão total sobre o ponto imerso sob a coluna será: $$P = \mu_{liq}.g.h+P_{atm}$$
Princípio de Pascal
O acréscimo de pressão dado a um ponto A transmite-se integralmente a todos os pontos do liquido, de tal forma: $$\frac{F_{1}}{A_{1}}=\frac{F_{2}}{A_{2}}$$
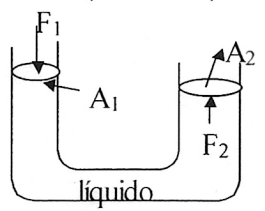
Empuxo
Todo corpo imerso, total ou parcialmente em um líquido recebe uma força vertical, de baixo para cima, denomidada empuxo: $$\vec{E} = \mu_{liq}.V_{imerso}.\vec{g}$$